Real‐space grid representation of momentum and kinetic energy operators for electronic structure calculations
Domenico Ninno; Giovanni Cantele; Fabio Trani
Index: 10.1002/jcc.25208
Full Text: HTML
Abstract
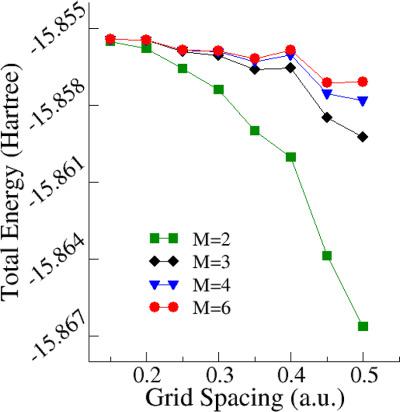
We show that the central finite difference formula for the first and the second derivative of a function can be derived, in the context of quantum mechanics, as matrix elements of the momentum and kinetic energy operators on discrete coordinate eigenkets defined on a uniform grid. Starting from the discretization of integrals involving canonical commutations, simple closed‐form expressions of the matrix elements are obtained. A detailed analysis of the convergence toward the continuum limit with respect to both the grid spacing and the derivative approximation order is presented. It is shown that the convergence from below of the eigenvalues in electronic structure calculations is an intrinsic feature of the finite difference method. © 2018 Wiley Periodicals, Inc.